Literature/202310101212 stereo darkfield interferometry
- Source: [[literature/@rieu2021Parallel, linear, and subnanometric 3D tracking of microparticles with Stereo Darkfield Interferometry|@rieu2021Parallel, linear, and subnanometric 3D tracking of microparticles with Stereo Darkfield Interferometry]]
- Tags: #Instrumentats #nanoparticle-tracking-analysis
One of the biggest issues with 3D nanoparticle tracking is that instruments lack sufficient resolution (both temporal and spatial). Stereo Darkfield Interferometry (SDI) solves some of the issues by using a combination of techniques in a "simple" to assemble microscope.
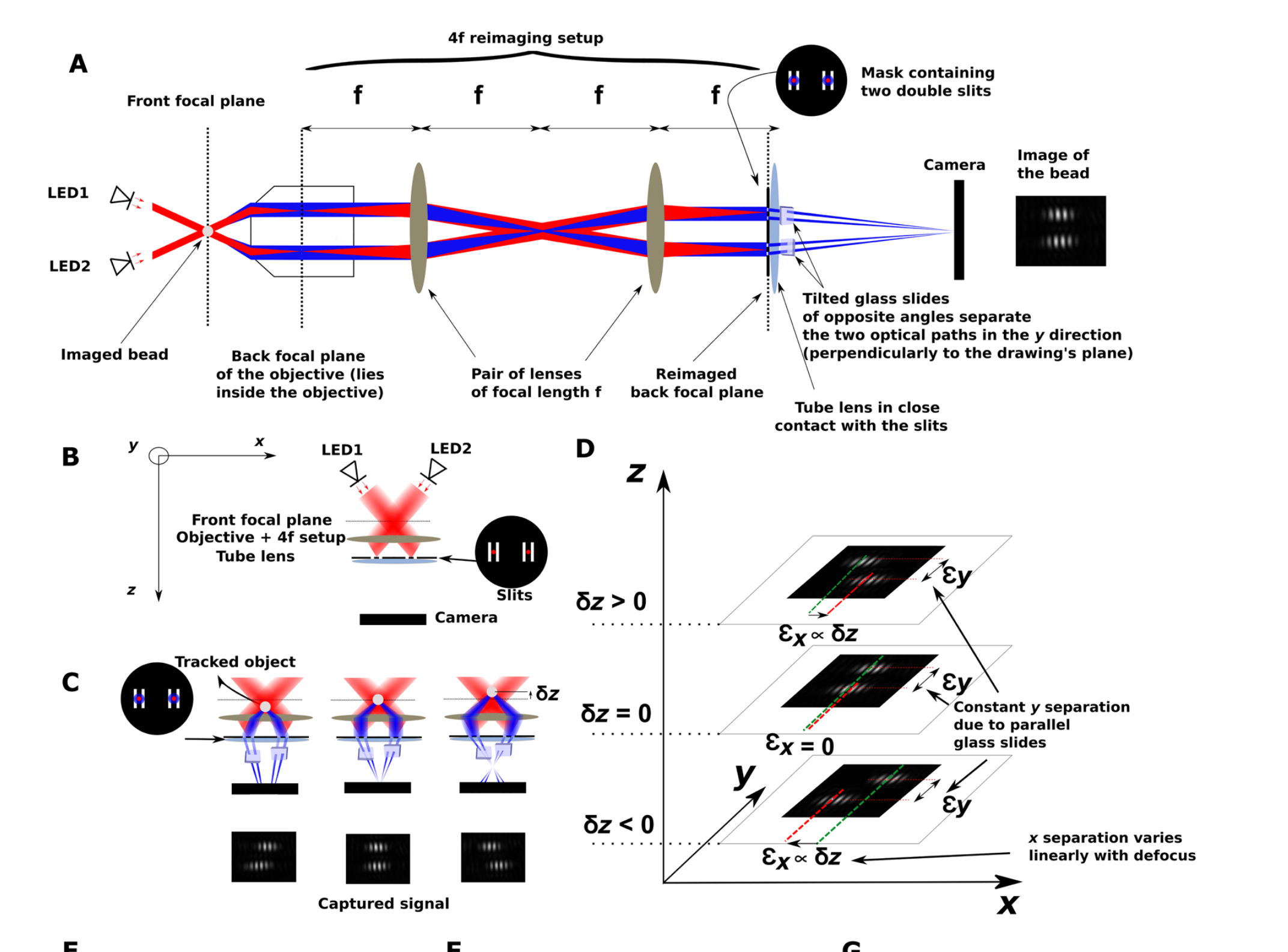
By adding a combination of a dark-field microscope (in the image above using two superluminescent LED's) with a slit configuration (right at the tube-lens), with two wedges that allow to separate the stereoscopic interference pattern, they can achieve full 3D localization with better than $nm$ accuracy.
I find it very interesting that the noise for the localization is given by:
$$ \sigma_i^2 > \frac{1}{g_i^2N}\frac{1}{\int \frac{f'(i)^2}{f(i)}di} $$
$g$ is related to the magnification, $N$ to the number of photons, but the interesting argument is the integral of the intensity profile ($f$). Since it depends on the derivative (squared!), the quicker the profile changes, the higher the precision.
Is perhaps these way of considering accuracy related to the way minflux works?
I also wonder if a method like this can be combined with a technique like SP-IRIS? In principle the interference pattern depends on the refractive index of the particle, which could be used for singe-shot sizing?
A different implementation, without the "stereo" is 202405221125 Nanofluidic Scattering Microscopy (NSM)
Backlinks
These are the other notes that link to this one.
Comment
