Literature/202212281435 polydisperse samples with inta
- Source: [[@kashkanova2022Precision size and refractive index analysis of weakly scattering nanoparticles in polydispersions]]
- Tags: #Refractive-Index #polydisperse-samples
Polydisperse Samples
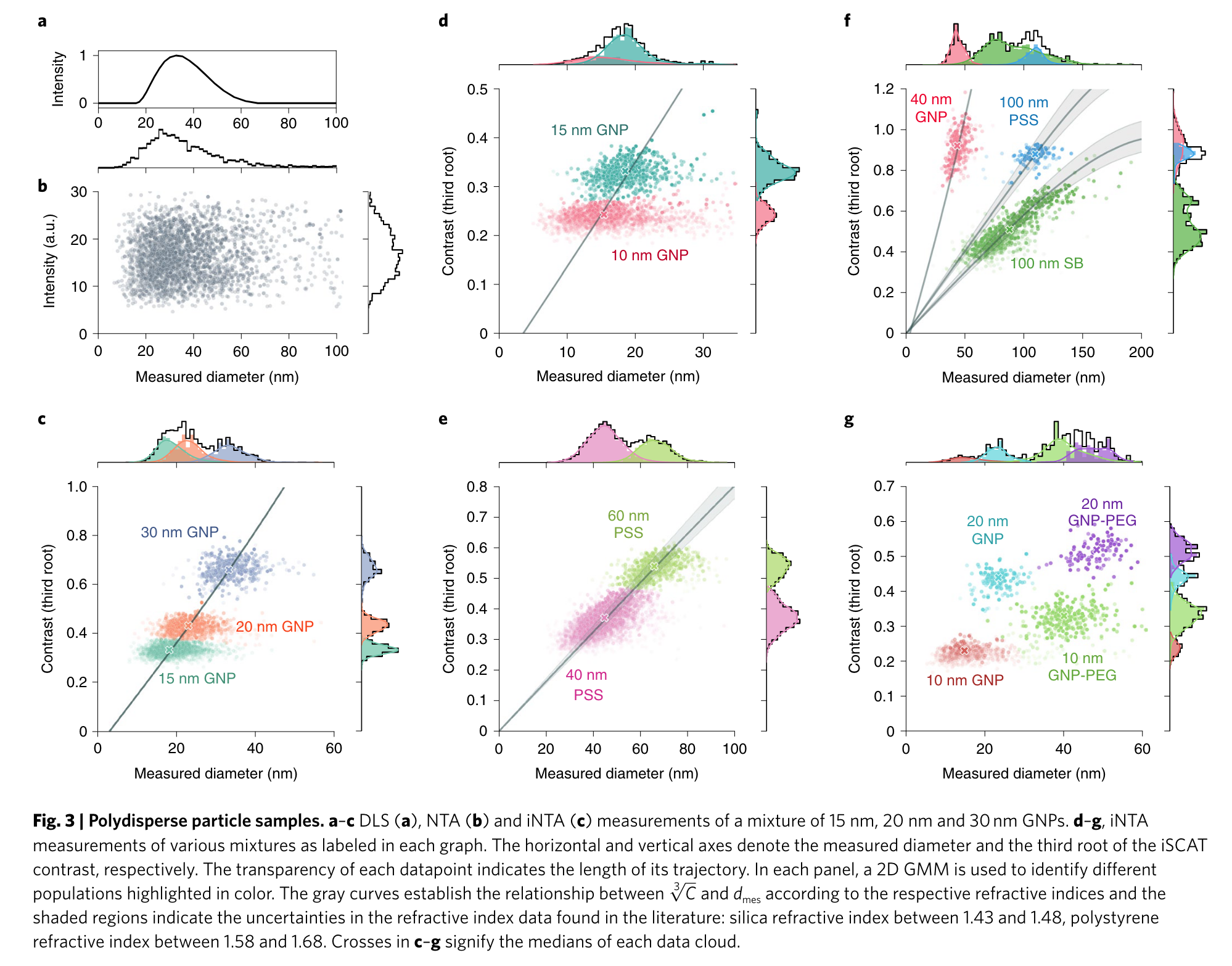
The paper makes a very clear case that for studying polydisperse samples, access to an accurate measurement of refractive index (or in the case of iNTA, contrast $C$) gives access to a better resolving power in two dimensions. It is clear that in some cases, like 15, 20, and 30nm gold particles, size alone is not enough to separate subpopulations, while the contrast is able to clearly distinguish between each other.
In order to create clusters of particles, they have implemented a Gaussian Mixture Model, which is an unsupervised machine learning model tool that fundamentally fits gaussian distributions of univariate samples.
The paper also points out that there's a difference between the hydrodynamic radius and the nominal radius of the sample. For the gold particles it is $l_H=1.8\pm 0.3 nm$ for all particle sizes, which becomes a 10% discrepancy for the smallest particles, and there's a chance that more complex samples will have larger hydration effects.
Backlinks
These are the other notes that link to this one.
