Determining the best number of fitting points for MSD data
- source: [ @ernst2013 Measuring a diffusion coefficient by single-particle tracking: statistical analysis of experimental mean squared displacement curves ]
- tags: #errors-nanoparticle-tracking-analysis
To measure the diffusion coefficient, we can fit the mean squared displacement curve with the following equation:
$$\textrm{MSD}(\tau) = 4\tilde{\textrm{D}}\tau^\alpha$$ Where $\tilde{\textrm{D}}$ is the generalized diffusion coefficient, and $\alpha$ depends on the diffusive process ($\alpha=1$ normal brownian, $\alpha>1$ superdiffusive, $\alpha<1$ subdifussive).
Experimentally, the accuracy of the MSD is limited, as well as the maximum $$\tau$$ possible. Therefore, it is valid to ask the question of what is the best approach to fit the data in order to extract the most accurate diffusion coefficient.
Considering more points does not necessarily improve the quality of the fit: the first few $\tau$ values are the result of the average over a large number of measurements, while the larger time delays are averaged only a couple of times.
In a setting where a single-particle is tracked over $10^5$ time-points, it is possible to divide the trajectory into different sub-sets and analyze how much the analysis changes compared to the analysis of the entire trajectory (presumably the most accurate one).
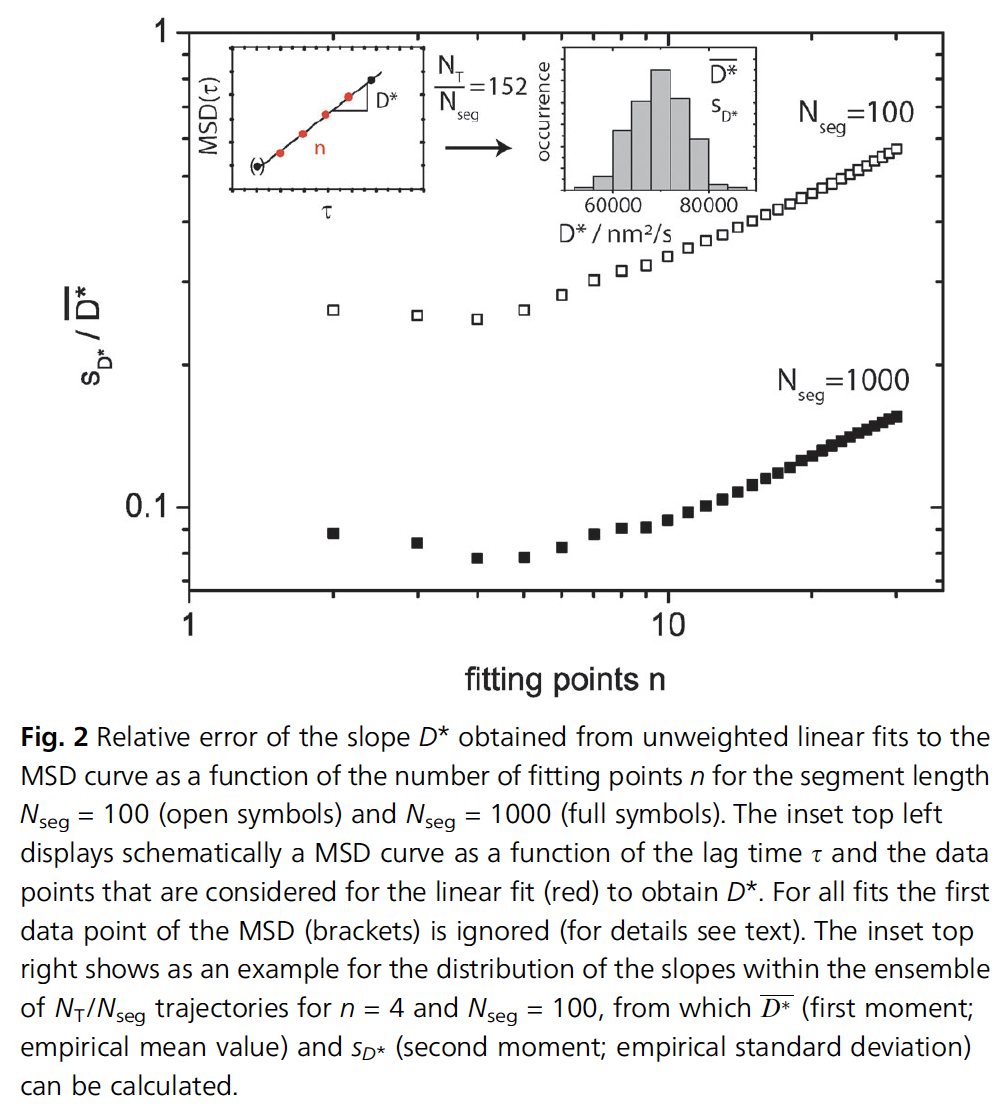
The figure above shows that using tracks of either $N=100$ or $N=1000$ points, the error in the determination of $\tilde{\textrm{D}}$ goes down initially, but after 4 or 5 fitting points, it increases dramatically. This means that the determination of the diffusion coefficient is best when using 4 or 5 points of $\tau$ and not the entire dataset.
Backlinks
These are the other notes that link to this one.
Comment
