The effect of the track length on the accuracy of the diffusion coefficient in MSD measurements
- source: @ernst2013 Measuring a diffusion coefficient by single-particle tracking: statistical analysis of experimental mean squared displacement curves
- tags: #errors-nanoparticle-tracking-analysis
The mean squared displacement of a particle’s trajectory can be useful to calculate its diffusion coefficient. The following equation:
$$\textrm{MSD}(\tau) = 4\tilde{\textrm{D}}\tau^\alpha$$
Can be used to extract the diffusion coefficient. Longer tracks should yield more accurate results, but the impact on track length is hard to quantify. Therefore, if the same particle is tracked over $$10^5$$ frames, it is possible to split the data into smaller datasets and study the impact on accuracy depending on the number of frames acquired.
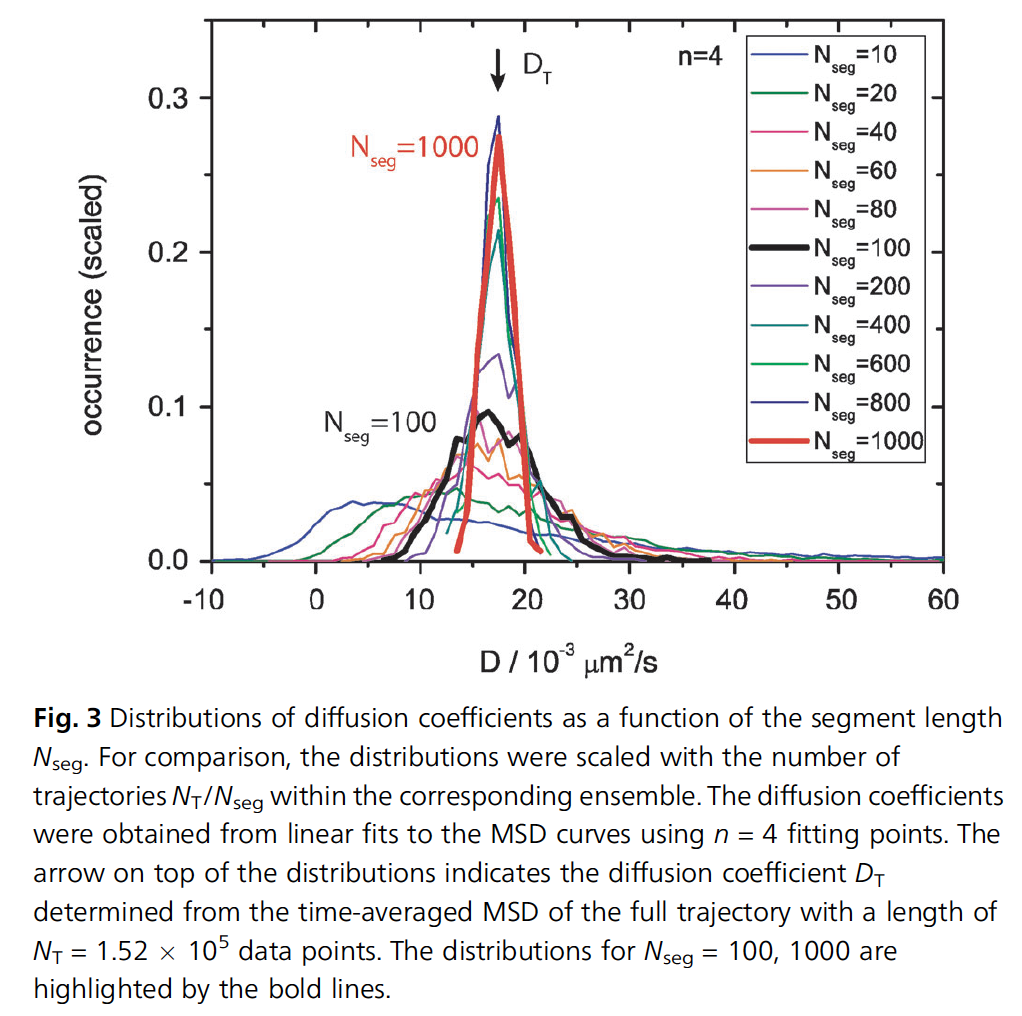
The figure above shows the uncertainty in the determination of the diffusion coefficient for different track lengths. The extration was done using the optimal number of time-delays (see: literature/202111291731 mean squared displacement errors ). For \(N=100\) the accuracy in the determination of the diffusion coefficient is of only \(\pm25\%\) . To get the accuracy down to \(\pm10\%\) we need to measure at least 1000 frames per particle.
Backlinks
These are the other notes that link to this one.
